Comment l'Homme s'est il inspiré de l'écureuil volant pour aboutir au modèle du wingsuit ?
Le wingsuit, un défi des lois de la physique
Tout d’abord il faut savoir que le wingsuiter et l’écureuil volant évoluent dans le fluide (milieu matériel déformable dans un état gazeux ou liquide) de l’air.
Lorsqu'ils effectuent un vol, ils défient plusieurs lois de la physique. En effet, quatre forces agissent sur leurs corps : le poids, la portance, la traînée et la poussée.
Evidemment entre l’Homme et l’écureuil volant les forces ne sont pas à la même échelle.
Ces lois de la physique doivent être méticuleusement étudiées par le wingsuiter pour éviter de faire un faux mouvement qui pourrait lui coûter la vie mais aussi pour lui permettre de planer parfaitement.
 CORE 2012 vol.jpg |  852748picturedsouthernflyingsquirrelc457diaporama.jpg |  |
|---|---|---|
 |  |  |
 |
Attirés vers le sol
Sur Terre comme tous corps ayant une masse, l'écureuil volant et l'Homme subissent la force du poids que l'on connaît tous.
Le poids est une force verticale qui s’applique sur le centre de gravité d’un corps en direction du centre de la Terre c'est à dire vers le sol.
Le poids est en fait une simplification de force de gravitation mis en évidence par Newton et sa célèbre pomme qui tombe d'un arbre, qui fait que par exemple, le wingsuiter et la Terre s’attirent.
La formule du poids est :

Sur Terre : g=~9.81 N.kg-1

On voit donc que le poids (P) dépend non seulement de la pesanteur (qui est fixe sur Terre) mais aussi de la masse (m). Il y a donc une différence de poids de l'écureuil volant par rapport à l'Homme.

"Portés" par l'air
Pour représenter le phénomène de portance voici deux vidéos, l'une d'un wingsuiter et une autre d'un écureuil volant :
On distingue bien cette force qui "porte" l'écureuil et le wingsuiter.
En effet, quand le wingsuiter ouvre les bras et écarte les jambes pendant la chute, la combinaison se gonfle d'air. Alors, la surface d'au-dessus, remplie d'air, aura une forme courbe et la surface d'en-dessous aura une forme plane. Il est alors "porté" par le fluide de l'air comme le montre cette vidéo.
Pour l'écureuil volant qui plane sur des plus petites distances, sa membrane seule suffit à provoquer cette force de portance.
L'Homme s'est donc ici inspiré de l'écureuil volant mais a ajouté une particularité à la combinaison pour que cette force soit suffisante pour le faire planer.
Pendant le vol, l'air arrive sur le wingsuit au bord d'attaque et se sépare en deux courants d'air : l'un traverse l'aile par la surface supérieure (extrados) et l'autre par la surface inférieure (intrados) du wingsuit.
Le fluide d'air contourne donc le corps du wingsuiter puis ressort par ce que l'on appelle le bord de fuite.
Le même phénomène est observé chez l'écureuil volant.

L'air qui passe par l'extrados va être d'une vitesse supérieure à la vitesse de l'air passant par l'intrados.
Cette différence de vitesse est expliquée par le fait que les deux courants d'air se séparant au bord d'attaque, se rejoignent en même temps au bord de fuite en parcourant chacun une distance différente.
Cela crée alors une dépression à l'extrados et une surpression à l'intrados.
Le wingsuit et l'écureuil vont donc être "attirés" vers le haut. Cette force est appelée la portance.

Pour effectuer un vol plus long le wingsuiter doit donc étudier cette force de portance.
Voici sa formule:

Le wingsuit se pratiquant dans le fuide de l'air, sa masse volumique (ρ) est donc en lien avec l'équation.
Plus la surface du wingsuit sera grande, plus sa chute sera ralentie, donc la surface est en lien avec la portance.
Plus la vitesse du wingsuit sera grande plus la dépression à l'extrados et la surpression à l'intrados sera importante et donc la portance aussi.
Le coefficient de portance varie selon l'angle d'incidence du wingsuit (voir schéma ci-dessous), plus il sera élevé, plus la portance sera importante.
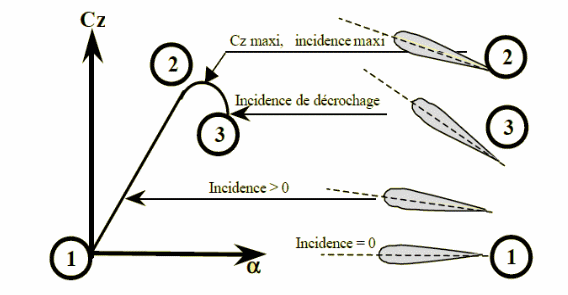
Donc pour que le wingsuiter ai une meilleur portance il faut que son angle d'incidence soit au maximum (numéro 2). En effet dans ce cas, son vol durera longtemps.
En revanche il ne faut pas que son angle d'incidence soit trop élevé sinon la portance n'agira plus sur lui (numéro 3).
En effet dans ce cas, le wingsuiter tombera en perdant tout contrôle sur son vol.
Nous n'avons pas trouvés pertinent de calculer cette force de portance car elle n'apporte pas une information essentielle et que la surface référente et le coefficient (qui ne peut être calculé qu'en soufflerie) varient selon chaque modèle de wingsuit.
En revanche cette équation nous a donc permis de savoir quels éléments sont à travailler sur le wingsuit afin de diminuer l'impact de la portance.
"Repoussés" par l'air
Voici deux vidéos pour représenter cette force qui "s'oppose horizontalement à la trajectoire du wingsuit et de l'écureuil volant et donc les ralentis dans leurs trajectoire :
On distingue que le wingsuiter et l'écureuil volant "luttent" contre le fluide de l'air. Cette force est communément appelée la traînée.
Plusieurs facteurs sont à l'origine de la traînée, nous allons les étudier afin de comprendre pourquoi le wingsuit et l'écureuil sont ralentis par ce fluide.
La traînée totale est constituée de plusieurs types de traînée :
La traînée de forme intervient dès qu’un objet d’épaisseur importante fait face au fluide de l'air
Ce type de trainée a donc peu d’effet car la combinaison de wingsuit a une forme étudiée et inspirée de l’écureuil volant pour pénétrer efficacement dans l'air sans induire une forte traînée de forme.
La traînée induite est dûe au phénomène de portance qui requiert une surpression à l'intrados et une dépression à l'extrados. Ainsi aux extrémités du wingsuit et de l’écureuil , la surpression de l'intrados veut combler la dépression de l'extrados.
Ce phénomène créé alors des tourbillons marginaux, c'est à dire des turbulences aux extrémités de la combinaison et de l’écureuil. Ces turbulences peuvent alors les ralentir.
En revanche cette traînée a très peu d’incidence sur la traînée totale car elle peut être facilement annulée. En effet le wingsuiter apprend à positionner ses bras de façon à ce que les ailes soient à l’horizontale et ainsi atténuer l’effet des tourbillons marginaux.
Quant à l’écureuil volant il le fait naturellement .

La traînée de frottement représente la plus grande partie de la traînée totale du wingsuit.
Le frottement du fluide de l’air sur toute la surface de l’écureuil ou du wingsuit provoque un ralentissement de ce fluide.
En effet, à l'endroit où se produit ce ralentissement , les molécules d’air sont ralenties ce qui a pour impact de diminuer la pénétration dans l'air du wingsuit et de l’écureuil.
Ces derniers seront alors ralentis comme le montre les vidéos.
Il n'y a donc que la traînée de frottement qui a un impact sur le wingsuiter et l’écureuil volant, en effet il n’existe aucun moyen pour la contrer contrairement aux autres forces de traînées qui s’exercent.
Cependant on peut porter des améliorations au wingsuit afin d’en diminuer l’impact, notamment en s’inspirant de la forme de l’écureuil volant.

Le wingsuiter doit donc avoir la forme la plus adéquate, afin de pénétrer correctement dans le fluide de l'air et donc limiter au maximum les frottement . Pour maîtriser et améliorer son vol, le wingsuiter doit donc manier parfaitement la force de traînée.
En voici la formule :

Avec :
T: valeur de la Traînée (en N)
ρ: masse volumique de l’air (en kg.m-3)
V: vitesse de déplacement (en m.s-1), en effet plus le wingsuit accélère plus la traînée sera forte.
S: surface de référence (en m²), plus la surface de la voile est importante plus la traînée sera forte.
Cx: coefficient de traînée (aucune unité), plus le wingsuit aura un profil approprié à la pénétration dans l'air, plus la traînée sera diminuée.
Le coefficient de traînée varie selon la forme du wingsuit :
En s'inspirant notamment de l'écureuil volant, la face avant du wingsuit est travaillée afin que le wingsuiter puisse entrer correctement dans le fluide de l'air. Mais il faut faire de même pour la face arrière, afin que les courants d'air se rejoignent correctement au bord de fuite.
Le coefficient de traînée varie donc à peu près de cette manière:
Nous n'avons pas trouvés pertinent de calculer cette force de traînée car elle n'apporte pas une information essentielle et que la surface référente et le coefficient (qui ne peut être calculer qu'en soufflerie) varient selon chaque modèle de wingsuit.
Cette équation nous a donc permis de savoir quelles choses sont à travailler sur le wingsuit afin de diminuer l'impact de la traînée.

"Poussés" vers l'avant
Naturellement le wingsuit et l’écureuil volant avancent dans le fluide de l’air. Dans le domaine de l’aviation cette force de poussée existe grâce aux réacteurs de l’avion.
Etant donné l’absence de réacteurs sur l’écureuil et le wingsuiter on se demande comment ils arrivent à aller de l’avant en plein vol si il n’y a pas de force de poussée.
En réalité, le wingsuiter et l’écureuil acquièrent une vitesse dès qu'ils sautent dans le vide. En effet, quand ils déploient leurs ailes lors de la chute, elles se gonflent d'air, ce qui est à l'origine de l'intervention de la portance vue précédemment. À ce moment précis, ils acquièrent une vitesse initiale qui les propulsent vers l'avant.
Les transferts d'énergies expliquent ce phénomène:
Il faut savoir que tout objet qui se déplace possède une énergie de mouvement. Cette dernière dépend de la vitesse et de la masse de l'objet. Cette énergie est appelée énergie cinétique (Ec).
Voici la formule de l'énergie cinétique:
Pour un wingsuiter de 80kg et allant à une vitesse de 150 km/h: Ec=1/2*80*41.67²
Ec=69456 J
Pour un écureuil volant de 190g allant à une vitesse de 10km/h : Ec=1/2*0.19*10²
Ec=9.5 J
Une autre énergie est aussi mise en évidence, c'est l'énergie de potentielle de pesanteur (Epp). Elle dépend de l'altitude de l'objet sur Terre. Plus l'objet sera haut plus il stockera cette énergie.
En revanche on ne peut constater cette énergie que quand l'objet se laisse tomber d'où le nom "potentielle" et donc bien entendu sera attiré par la Terre grâce à la "pesanteur".
Voici la formule de l'énergie potentielle de pesanteur: m: masse de l'objet (en kg)
g: intensité de pesanteur (=9.81N.kg-1)
z: altitude de l'objet (en m)
Pour le même wingsuiter sautant d'une montagne à 2000m d'altitude: Epp=80*9.81*2000
Epp=1569600 J
Et pour le même écureuil volant sautant d'un arbre à 10m d'altitude: Epp=0.19*9.81*10
Epp=18.64 J
La somme de ces deux énergies forme l'énergie mécanique (E). Au cours du mouvement d'un objet, son énergie potentielle de pesanteur est donc convertie en énergie cinétique.
Pour le wingsuiter : Em=69456+1569600 Pour l'écureuil volant: Em=9.5+18.64
Em=1708512 J Em=28.14 J
Ce graphique présente l'évolution des ces trois énergies sans ordre de grandeur lors d'un vol de wingsuit ou d'écureuil volant.

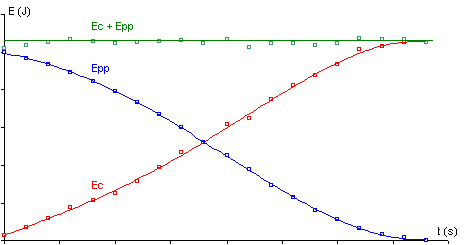
Ce sont donc les transferts d’énergies qui sont à l’origine de cette, en effet l’énergie potentielle de pesanteur qu'ils engrangent en se plaçant en haut d’une montagne pour le wingsuit ou d’un arbre pour l’écureuil se transforme en énergie cinétique et donc acquièrent cette vitesse initiale.
La finesse, un rapport primordial
Le wingsuit défie donc les lois de la physique en voulant réaliser le meilleur vol possible : le moins possible de traînée et une meilleur portance pour parcourir une plus grande distance.
Le rapport Portance/Traînée est appelé finesse et représente le nombre de mètres parcourus horizontalement pour le nombre de mètres perdus verticalement. Généralement, les wingsuits atteignent une finesse moyenne de 3 et de 4 pour les plus récent .